El concepto de validez deductiva

Antes he dicho que la lógica formal o deductiva se ocupa de los argumentos desde el punto de vista de la corrección formal de estos. Pero ¿qué significa esto con más precisión? Para aclararlo partiré de algo que es obvio, a saber, que no sólo se argumenta en contextos jurídicos, sino también en el ámbito de los diversos conocimientos especializados y en el de la vida cotidiana.

También en la literatura nos encontramos con cierta frecuencia con argumentaciones aunque, desde luego, la función principal de las obras literarias no es la de registrar argumentos, sino más bien la de expresar sentimientos, narrar historias, fabular, etc. Sin embargo, hay un género literario especialmente denso en argumentaciones; se trata del género policiaco, cuyo inventor habría sido Edgard Allan Poe. Uno de sus cuentos más célebres lleva por título La carta robada, y en el mismo se narra una historia que aproximadamente es la siguiente:

Auguste Dupin (el precursor de Shelock Holmes, el padre Brown, Hércules Poirot, etc.) recibe un día la visita del prefecto de la policía de París, que le consulta sobre el siguiente problema. Un documento de la mayor importancia ha sido robado de las habitaciones reales. Se sabe que el autor del robo es el ministro D., quien usa la carta como instrumento de chantaje contra la dama que la redacta. El ministro debe tener la carta oculta en algún lugar de su casa, pero el prefecto, a pesar de haber efectuado un minucioso y sistemático registro, no logra dar con ella. Dupin consigue hacerlo merced a un proceso de razonamiento, que, grosso modo, es el siguiente: si la carta hubiese estado al alcance de la búsqueda, los agentes la habrían descubierto, y, como la carta tiene que encontrarse en el domicilio del ministro, ello quiere decir que la policía ha buscado mal. Dupin sabe que el ministro es una persona audaz e inteligente y que, además, posee no solamente una inteligencia matemática, sino también -si se puede llamar así- una inteligencia poética. El ministro pudo prever, por tanto, que su casa iba a ser registrada por la policía y que los hombres del prefecto buscarían en todos aquellos sitios en donde se supone que uno puede dejar un objeto que desea ocultar. De ahí infiere Dupin que el ministro tuvo que dejar la carta en un lugar muy visible pero, precisamente por ello, inesperado. Y, en efecto, Dupin encuentra la carta en una tarjeta de cartón que colgaba de una cinta azul sobre la chimenea, arrugada y manchada (como si se tratara de algo sin importancia) que exhibía un tipo de letra en la dirección y un sello de características opuestas a las de la carta robada (pues la misma había sido dada la vuelta como un guante). Dupin explica así el fracaso del prefecto: “La causa remota de su fracaso es la suposición de que el ministro es un imbécil porque ha logrado fama de poeta. Todos los imbéciles son poetas; así lo siente el prefecto e incurre en una non distributio medii al inferir que todos los poetas son imbéciles”.

Así, de acuerdo con el relato, el prefecto ha cometido un error de tipo lógico, una falacia, pues de la afirmación: Todos los imbéciles son poetas, no se infiere lógicamente: Todos los poetas son imbéciles. A partir de esta afirmación, el prefecto ha efectuado un argumento lógicamente válido, pero con una premisa falsa:

En la lógica proposicional, la inferencia podría representarse aproximadamente, así:

Y, con más precisión, en la lógica de predicados de primer orden:

El argumento en cuestión es lógicamente válido porque la conclusión se infiere necesariamente de las premisas. Esto es fácil de ver gráficamente. Si simbolizamos con P la clase de los poetas, con I la de los imbéciles y con m al ministro (m, señalado en el gráfico con un punto, designa a un individuo, mientras que P e I designan clases o conjuntos de individuos), la información que se contiene en las dos premisas del argumento la podemos representar así:

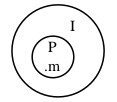
Si ahora quisiéramos representar también la información de la conclusión, nos daríamos cuenta de que no necesitamos añadir nada: la información de la conclusión estaba ya incluida en la de las premisas, lo que explica que hayamos podido decir que el paso de unas a otra fuera necesario; o sea, no es posible que las premisas sean verdaderas y la conclusión no lo sea.

Mientras que a) es un ejemplo de argumento válido lógicamente, pero con una premisa falsa, el siguiente argumento, b), representa casi el caso opuesto, es decir, aquel en que las premisas son verdaderas (verdaderas, naturalmente, en relación con el cuento de Poe), pero el argumento es lógicamente inválido. En concreto, se trata de la falacia denominada de afirmación del consecuente:

Y en notación lógica:

Para comprobar que, efectivamente, es un argumento lógicamente incorrecto o inválido, podemos someterlo a la misma prueba de antes. Ahora bien, una representación que está de acuerdo con la información contenida en las premisas podría ser esta:

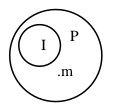
Y, sin embargo, esta resulta incompatible con la información que transmite la conclusión. Por lo tanto, en este caso sí es posible que las premisas sean verdaderas, pero la conclusión falsa.

Antes se ha dicho que a) y b) eran casos casi opuestos. Si no son del todo opuestos es porque, en ambos, la conclusión, que es la misma, es falsa. En el siguiente ejemplo, c), tanto las premisas como la conclusión son verdaderas; sin embargo, no se trata de un argumento lógicamente válido.

Para probar su invalidez lógica, bastará con efectuar de nuevo una representación posible de la información contenida en las premisas

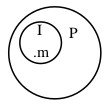
que, sin embargo, contradice la información de la conclusión.

Finalmente, un ejemplo de argumento válido lógicamente y cuyas premisas son verdaderas (y, por tanto, también su conclusión) sería este:

En este caso, cualquier posible representación de las premisas contendría también la conclusión. Así, una manera de representar la información contenida en las premisas sería esta:

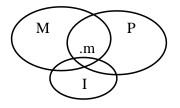
en la que, obviamente, se contiene también la información de la conclusión.

Ahora estamos, sin duda, en condiciones de entender mejor la noción de argumento lógico que puede definirse de la siguiente manera: “Tenemos una implicación o una inferencia lógica o una argumentación válida (deductivamente), cuando la conclusión necesariamente es verdadera si las premisas son verdaderas”.

La lógica, la lógica deductiva, puede presentarse en forma axiomática o como un sistema de reglas de inferencia, pero esta segunda forma de presentación es la que mejor se ajusta a la manera natural de razonar. Ello es así porque mientras que en el modo axiomático de deducir se parte de enunciados formalmente verdaderos (tautologías) y se llega, al cabo de la deducción, a enunciados también formalmente verdaderos, en el modo natural de hacer inferencias deductivas se puede partir -y eso es lo más frecuente- de enunciados con valor de verdad indeterminado o incluso declaradamente falsos, y se llega a enunciados que pueden ser verdaderos o falsos. Lo único que determina una regla de inferencia es que si las premisas son verdaderas, entonces también tienen que serlo necesariamente la conclusión.

Los razonamientos indicados con a) y d) y los esquemas lógicos correspondientes son válidos en virtud de la regla llamada modus ponens, que se puede escribir así:

El uso de las letras X y Y se debe a que las reglas se expresan en un metalenguaje en relación con el de las fórmulas de la lógica para el que empleamos las letras p, q, P, Q, etc.

Por el contrario, los razonamientos b) y c) y los esquemas correspondientes son inválidos lógicamente, porque no hay ninguna regla de inferencia lógica que autorice efectuar el paso que en ellos se da.